spiral arms – Jaehan Bae

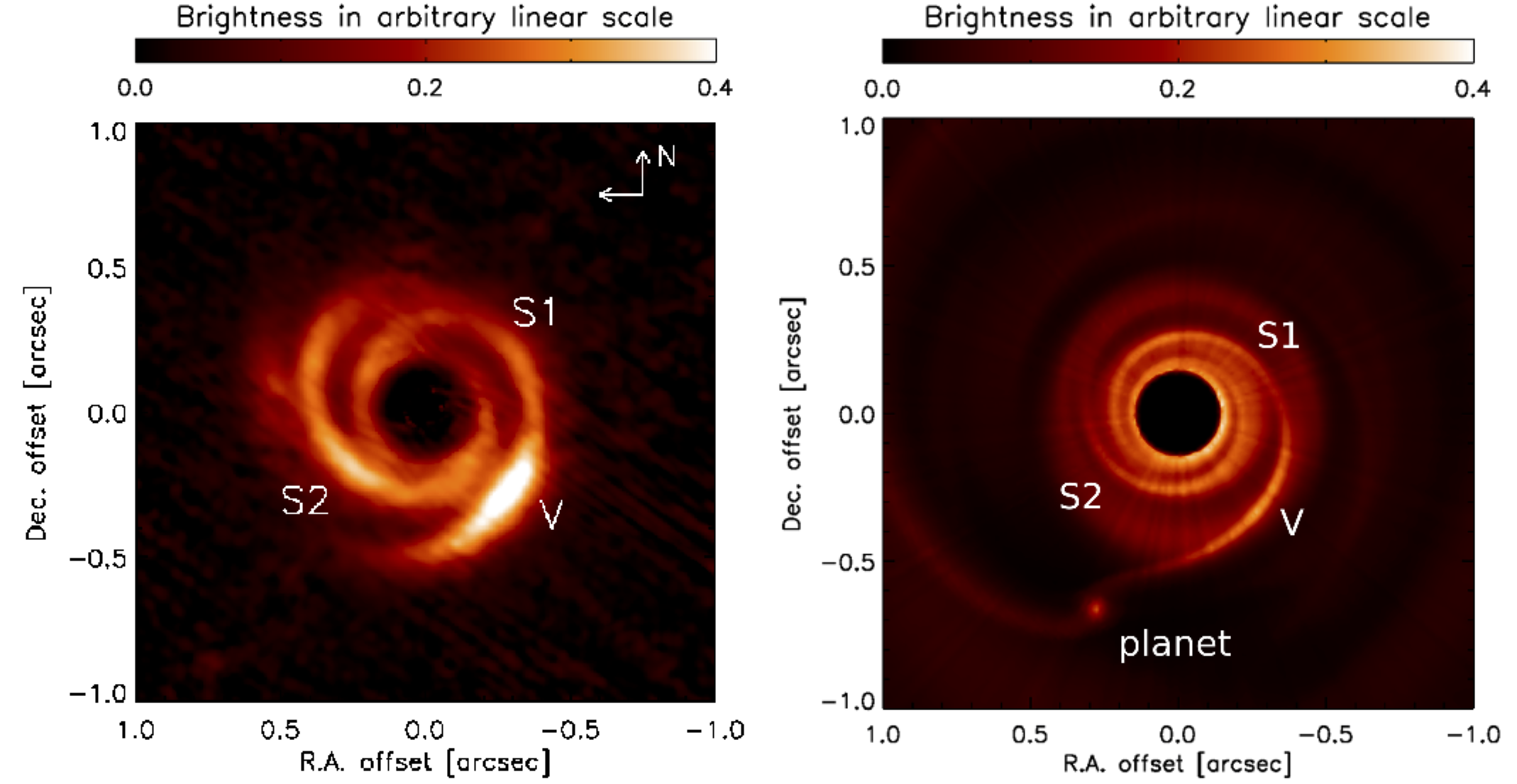
Another interesting structure revealed in protoplanetary disks with state-of-the-art telescopes is spiral arms. On the left in the above figure is a scattered light image of the SAO 206462 disk (Garufi et al. 2013). We are looking at the photons which are originally emitted by the central star but then scattered off the surface of the disk toward us. On the right is my attempt to reproduce the observation with a planet in the disk (Bae et al. 2016a). The planet excites two spiral arms (S1 and S2) interior to its orbit. A vortex (V) forms at the inner edge of the gap opened by the planet. At this snapshot, one of the spiral arms (S1) passes through the vortex (V), and this is how we interpret the bright blob V in the observation.

Now, how does a planet excite multiple spiral arms? To make things simple, let’s consider a very small mass planet, say a few Earth-mass planet around a solar-mass star, for which we can safely ignore non-linear effects. The gravitational potential of the planet can be decomposed into a Fourier series, a sum of individual azimuthal modes having different azimuthal wavenumbers \(m\) \(=1\), \(…\), \(\infty\). Each individual azimuthal mode excites \(m\) wave modes at its Lindblad resonance, which is known for many decades since a series of seminal papers by Goldreich & Tremaine (1978a,b, 1979).

Before I move forward, I have some examples in the figure below to help you visualize how this works. In the figure the potential of the planet is centered at \((X,Y)=(1,0)\) and what I’ve plotted here is the surface density distributions perturbed by individual azimuthal modes of the Fourier decomposed potential with \(m=2\), \(3\), \(4\), and \(5\). For the left panel, for example, I’m showing a result from a simulation in which I included only \(m=2\) azimuthal mode of planet’s potential. As shown, an \(m\)th azimuthal mode excites \(m\) spiral wave modes, which are indicated with \(n=0\), \(1\), …, \(m-1\). I show only four different \(m\)s but you can imagine the same happens for any given \(m\).

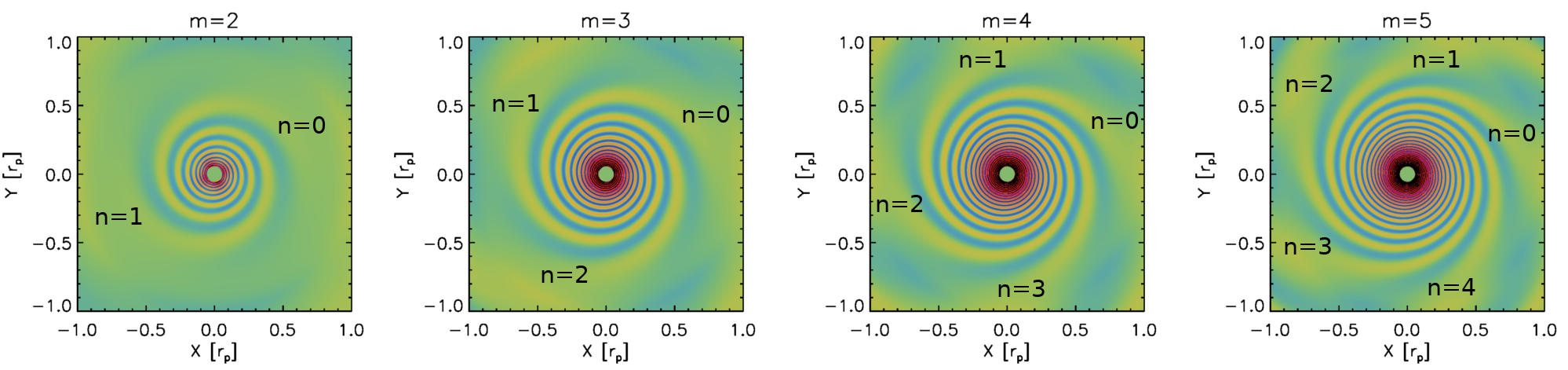
Now, what I’m going to do is to plot \(n=0\) components having different azimuthal wavenumbers.

As shown in the above movie, \(n=0\) components are closely located to each other, except for a couple of wave modes with the smallest \(m\)s. This raises a possibility that these wave modes can be constructively interfere each other, creating a coherent structure: a spiral arm. The next two movies will plot \(n=1\) and \(n=2\) components and you will see that these sets of wave modes can create spiral arms in a similar manner. The main difference in non-zero \(n\) components is that wave modes excite (significantly) out of phase. However, the propagation of wave modes depends on their wavenumber \(m\) such that they can become in phase to be constructively added together.

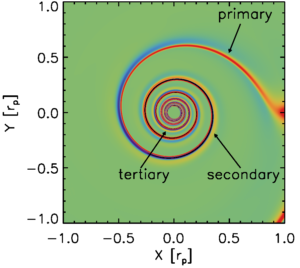
When non-linear effects can be ignored we can simply add up the perturbations driven by individual modes to reconstruct the perturbation driven by the full potential of the planet. When we do this, you will see three spiral arms emerge, as the above movies suggest. The primary spiral arm, the one directly attached to the planet, forms from superposition of the \(n=0 \) components in the above Fourier representation. Similarly, the secondary and tertiary arms form from superposition of the \(n=1\) and \(n=2\) components, respectively. See also an animated version here, in which I add the perturbations driven by individual modes one at a time from \(m=1\) to \(m=30\).

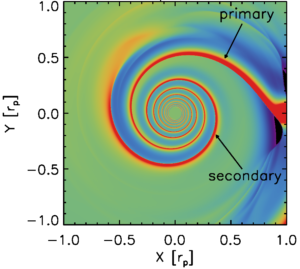
I understand that the three spiral arms are very tightly wound and do not really look like the ones we have observed so far. That’s true and it’s probably because the planets responsible for the observed spiral arms are much more massive than the one used in this example. Non-linear effects become increasingly important as the planet mass increases. For a larger mass planet spiral arms are more opened and the separation between the spirals increases. See the snapshot below for two-armed spirals excited by a 3 Jupiter-mass planet. Doesn’t this look more similar to the spiral arms you know of?